ЕГЭ по алгебреЕГЭ по алгебреЭкзаменационная
работа по математике состоит из 25 заданий,
которые разделены на 2 части. Часть 1
содержит 12 несложных заданий с выбором
ответа. Часть 2 состоит из 13 более сложных
заданий разного типа: 10 - с кратким ответом (из
одного числа) и 3 - с развёрнутым ответом.
К
каждому из 12 первых заданий работы даны 4
варианта ответа, из которых один верный. При
их выполнении надо выбрать правильный
ответ и занести его в бланк.
При
выполнении заданий 13-22 надо дать краткий
ответ из одного числа. В конце работы даны 3
задания (23, 24 и 25), на которые надо дать
развернутый ответ.
Внимательно
читайте каждый вопрос и предлагаемые
варианты ответа. Отвечайте только после
того, как Вы поняли вопрос,
проанализировали все варианты ответа и
выполнили необходимые вычисления.
На
выполнение работы отводится 3 часа (180 минут).
Рекомендуем выполнять задания в том
порядке, в котором они даны в работе. Если
какое-то задание у вас вызывает затруднение,
то пропустите его и постарайтесь выполнить
те, в которых вы уверены. К пропущенному
заданию можно вернуться, если у вас
останется время.
ВАЖНО!
Для получения оценки "5" НЕ ТРЕБУЕТСЯ
выполнять все задания работы.
ВАЖНО!
Для получения положительной оценки "3"
ДОСТАТОЧНО верно выполнить любые 15 заданий
из Части 1 или любые 15 заданий из работы в
целом.
ТЕСТ
ПО МАТЕМАТИКЕ (Часть 1)
1.
Найдите значение выражения
Ответ:
2.
Упростите выражение cos(p-x)
+ sin(1,5p+x)
- 2cos(2p-x)
Ответ:
0
sin(x) - cos(x)
-2cos(x)
-4cos(x)
3.
Выполните действия
Ответ:
4.
Упростите выражение log648 - log64 + log63
Ответ:
47
36
2
4
5.
Решите неравенство log3(x-3) > log3(4-x)
Ответ:
(3;
4)
(3,5;
4)
(3; +¥)
(3,5;
+¥)
6.
Решите неравенство
Ответ:
[13;
+¥)
[-2;
3)È(13;
+¥)
(-2;
3]È[13;
+¥)
(-2;
3)È[13;
+¥)
7.
Найдите область определения функции
Ответ:
(-¥;
2]
[2; +¥)
[4; +¥)
(-¥;
4]
8.
Найдите область значений функции y=2sin(x) + 1
Ответ:
[-1;
3]
[-2;
3]
[2;
3]
[-1;
2]
9.
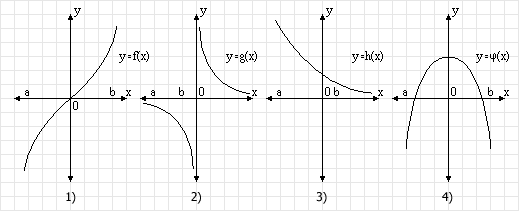
Какие
функции возрастают на промежутке [a; b] ?
Ответ:
1
2
3
4
10.
Найдите значение производной функции y=f(x) в
точке x0.
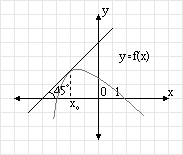
Ответ:
-2
2
-1
1
11.
Найдите производную функции h(x) = x2 + 3sin(x)
Ответ:
h'(x)
= x3 - 3cos(x)
h'(x) = 2x + 3cos(x)
h'(x) = 2x + cos(x)
h'(x) = (1/3)x3 - cos(x)
12.
Для функции f(x) = -3cos(x) укажите первообразную,
которая проходит через точку
Ответ:
F(x) = 3cos(x) - 12
F(x) = 3sin(x) - 9
F(x) = -3sin(x) - 9
F(x) = 3sin(x) - 12
ТЕСТ
ПО МАТЕМАТИКЕ (Часть 2)
Задания
13-22 требуют краткого ответа из одного числа.
13.
Найдите корни уравнения, 2cos(x) - cos2(x) = sin2(x)
принадлежащие промежутку [0°;
270°].
Ответ:
14.
Найдите точку максимума функции f(x) = 2x3
+ 3x2
Ответ:
15.
Найдите наименьший корень уравнения 2|x +
4| - 8 = 0
Ответ:
16.
Острый угол ромба равен 60°,
а площадь -
м2.
Найдите меньшую диагональ ромба.
Ответ:
17.
Вычислите значение произведения х*у, где (х;
у) - решение системы уравнений
Ответ:
18.
Теплоход прошел расстояние от А до В по
течению реки за 7 ч, а от В до А - за 14 ч. За
какое время проплывет от А до В плот?
Ответ:
19.
Вычислите значение выражения
Ответ:
20.
Найдите наибольшее значение функции
Ответ:
21.
Высота правильной четырехугольной
пирамиды равна 4 м, а боковое ребро -
м.
Найдите площадь сферы, вписанной в пирамиду
(число p
считайте равным 3)
Ответ:
22.
Найдите наибольшее целое значение
параметра а, при котором функция
f(x)
= ax2 - x3 - 3ax - 1 убывает на
множестве всех действительных чисел.
Ответ:
При
выполнении заданий 23-25 надо записать
развернутый ответ с объяснением.
23.
Решите неравенство (2 - |x - 1|)log0.1(4x2
+ 8) <
0
Ответ:
24.
Найдите нули функции h(x) = 6x + x2 - x3
-
Ответ:
25.
Вычислите значение выражения
